内核数据结构

发表于 分类于 ， ， ， 阅读次数： 本文字数： 21k 阅读时长 ≈ 19 分钟

本章将介绍几种Linux内核常用的内建数据结构。和其他很多大型项目一样，Linux内核实现了这些通用数据结构，而且提倡大家在开发时重用。内核开发者应该尽可能地使用这些数据结构，而不要搞自作主张地山寨方法。在下面的内容中，我们讲述这些通用数据结构中最有用的几个。

  1. 链表
  2. 队列
  3. 映射
  4. 二叉树

最后还要讨论算法复杂度，以及何种规模的算法或者数据结构可以相对容易的支持更大的输入集合。

链表

链表是Linux内核中最简单、最普通的数据结构。链表是一种存放和操作可变数量元素（常称为节点）的数据结构。链表和静态数组的不同在于，它所包含的元素都是动态创建并插入链表的，在编译时不必知道具体需要创建多少个元素。另外也因为链表中每个元素的创建时间各不相同，所以它们在内存中无需占用连续内存区。正是因为元素不连续的存放，所以各元素需要通过某种方式被连接在一起。于是每个元素都包含一个指向下一个元素的指针，当有元素加入链表或从链表删除元素时，简单调整指向下一个节点的指针就可以了。

单向链表和双向链表

可以用一种简单的数据结构来表示这样一个链表：

1
2
3
4
5
//一个链表中的一个元素
struct list_element {
    void *data;                 //有效数据
    struct list_elemet *next;   //指向下一个元素的指针
};

下图描述一个链表结构体。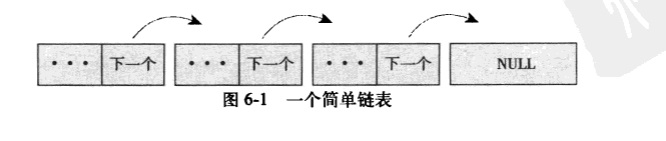
img not found
在有些链表中，每个元素还包含一个指向前一个元素的指针，因为它们可以同时向前和向后相互连接，所以这些链表被称作双向链表。而上图那种只能向后连接的链表被称作单向链表。
表示双向链表的一种数据结构如下：

1
2
3
4
5
6
//一个链表中的一个元素
struct list_element {
    void *data;                 //有效数据
    struct list_elemet *next;   //指向下一个元素的指针
    struct list_elemet *prev;   //指向上一个元素的指针
};

下图描述了一个双向链表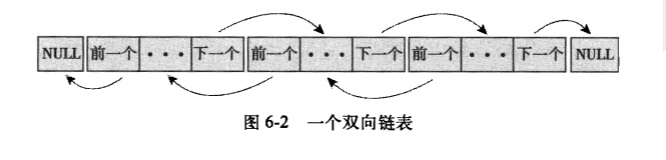
img not found

环形链表

通常情况下，因为链表中的最后一个元素不再有下一个元素，所以将链表尾元素中的向后指针设置为NULL，以此表明它是链表中的最后一个元素。但在有些链表中，末尾元素并不指向特殊值，相反，它指回链表的首元素。这种链表因为首尾相连，所以被称为是环形链表。环形链表也存在双向链表和单向链表两种形式。在环形双向链表中，首节点的向前指针指向尾节点。下图分别表示单向和环形双向链表：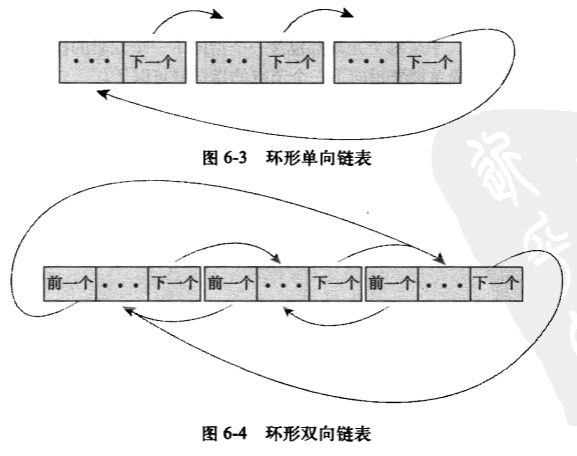
img not found
因为环形双向链表提供了最大的灵活性，所以Linux内核的标准链表就是采用环形双向链表形式实现的。

沿链表移动

沿链表移动只能是线性移动。先访问某个元素，然后沿该元素的向后指针访问下一个元素，不断重复这个过程，就可以沿链表向后移动了。这是一种最简单的沿链表移动方法，也是最适合访问链表的方法。如果需要随机访问数据，一般不使用链表。使用链表存放数据的理想情况是，需要遍历所有数据或需要动态加入和删除数据时。
有时，首元素会用一个特殊指针表示–该指针称为头指针，利用头指针可方便、快速地找到链表地“起始端”。在非环形链表里，向后指针指向NULL的元素是尾元素，而在环形链表里向后指针指向头元素的元素是尾元素。遍历一个链表需要线性地访问从第一个元素到最后一个元素之间的所有元素。对于双向链表来说，也可以反向遍历链表，可以从最后一个元素线性访问到第一个元素。当然还可以从链表中的指定元素开始向前和向后访问数个元素，并不一定要访问整个链表。

Linux内核中的实现

相比普遍的链表实现方式（包括前面章节描述的通用方法），Linux内核的实现可以说是独树一帜。回忆早先提到的数据（或者一组数据，比如一个struct）通过在内部添加一个指向数据的next节点指针，才能串联在链表中。比如，假定我们有一个fox数据结构来描述犬科动物中的一员。

1
2
3
4
5
struct fox {
    unsigned long   tail_length;    //尾巴长度
    unsigned long   weight;         //重量
    bool            is_fantastic;   //这只狐狸奇妙吗？
};

存储这个结构到链表里的通常方法是在数据结构中嵌入一个链表指针，比如：

1
2
3
4
5
6
7
struct fox {
    unsigned long   tail_length;    //尾巴长度
    unsigned long   weight;         //重量
    bool            is_fantastic;   //这只狐狸奇妙吗？
    struct fox      *next;          //指向下一只狐狸
    struct fox      *prev;          //指向上一只狐狸
};

Linux内核方式与众不同，它不是将数据结构塞入链表，而是将链表节点塞入数据结构。

链表数据结构

在过去，内核中有许多链表的实现，该选一个即简单、又高效的链表来统一它们了。在2.1内核开发系列中，首次引入了官方内核链表实现。从此内核中的所有链表现在都使用官方的链表实现了，千万不要自己造轮子拉！
链表代码在头文件<linux/list.h>中声明，其数据结构很简单：

1
2
3
4
struct list_head {
    struct list_head *next;
    struct list_head *prev;
};

next指针指向了下一个链表节点，prev指针指向前一个。然而，似乎这里还看不出它们有多大的作用。到底什么才是链表存储的具体内容呢？其实关键在于理解list_head结构是如何使用的。

1
2
3
4
5
6
struct fox {
    unsigned long       tail_length;    //尾巴长度
    unsigned long       weight;         //重量
    bool                is_fantastic;   //这只狐狸奇妙吗？
    struct list_head    list;           //所有fox结构体形成链表
};

上述结构中，fox中的list.next指向下一个元素，list.prev指向前一个元素。现在链表已经能用了，但是显然还不够方便。因此内核又提供了一组链表操作例程。比如list_add()方法加入一个新节点到链表中。但是，这些方法都有一个统一的特点：它们只接受list_head结构作为参数。使用宏container_of()我们可以很方便的从链表指针找到父结构中包含的任何变量。这是因为在C语言中，一个给定结构中的变量偏移在编译时地址就被ABI固定下来了。

1
2
3
#define container_of(ptr, type, member) ({                  \
	const typeof( ((type *)0)->member ) *__mptr = (ptr);    \
	(type *)( (char *)__mptr - offsetof(type,member) );})

使用container_of()宏，我们定义了一个简单的函数便可以返回包含list_head的父类型结构体：

1
2
#define list_entry(ptr,type,member) \
    container_of(ptr,type,member)

依靠list_entry()方法，内核提供了创建、操作以及其他链表管理的各种例程–所有这些方法都不需要知道list_head所嵌入对象的数据结构。

定义一个链表

正如看到的：list_head本身其实并没有意义–它需要被嵌入到你自己的数据结构中才能生效：

1
2
3
4
5
6
struct fox {
    unsigned long       tail_length;    //尾巴长度
    unsigned long       weight;         //重量
    bool                is_fantastic;   //这只狐狸奇妙吗？
    struct list_head    list;           //所有fox结构体形成链表
};

链表需要在使用前初始化。因为多数元素都是动态创建的（也许这就是需要链表的原因），因此最常见的方式是在运行时初始化链表。

1
2
3
4
5
6
struct fox *red_fox;
red_fox = kmalloc(sizeof(*red_fox),GFP_KERNEL);
red_fox->tail_length = 40;
red_fox->weight = 6;
red_fox->is_fantastic = false;
INIT_LIST_HEAD(&red_fox->list);

如果一个结构在编译期静态创建，而你需要在其中给出一个链表的直接引用，下面是最简方式：

1
2
3
4
5
struct fox red_fox = {
    .tail_length = 40,
    .weight = 6,
    .list = LIST_HEAD_INIT(red_fox.list),
};

链表头

前面我们展示了如何把一个现有的数据结构（这里是我们的fox结构体）改造成链表。
简单修改上述代码，我们的结构便可以被内核链表例程管理。但是在可以使用这些例程前，需要一个标准的索引指针指向整个链表，即链表的头指针。
内核链表实现中最杰出的特性就是：我们的fox节点都是无差别的–每一个都包含一个list_head指针，于是我们可以从任何一个节点起遍历链表，直到我们看到所有节点。这种方式确实很优美，不过有时确实也需要一个特殊指针索引到整个链表，而不是从一个链表节点触发。有趣的是，这个特殊的索引节点事实上也就是一个常规的list_head：

1
static LIST_HEAD(fox_list);

该函数定义并初始化了一个名为fox_list的链表例程，这些例程中的大多数都只接受一个或者两个参数：头节点或者头节点加上一个特殊链表节点。下面我们就看看这些操作例程。

操作链表

内核提供了一组函数来操作链表，这些函数都要使用一个或多个list_head结构体指针作参数。因为函数都是C语言以内联函数形式实现的，所以它们的原型在文件<linux/list.h>中。
有趣的是，所有这些函数的复杂度都为O（1）。这意味着，无论这些函数操作的链表大小如何，无论它们得到的参数如何，它们都在恒定的时间内完成。比如，不管是对于包含3个元素的链表还是对于包含3000个元素的链表，从链表中删除一项或者加入一项花费的时间都是相同的。这点可能没有什么让人惊奇的，但你最好还是搞清楚其中的原因。

向链表中增加一个节点

给链表增加一个节点：

1
list_add(struct list_head *new,struct list_head *head)

该函数向指定链表的head节点后插入new节点。因为链表是循环的，而且通常没有首位节点的概念。所以你可以把任何一个节点当成head。如果把“最后”一个节点当成head的话，那么该函数可以用来实现一个栈。
回到我们的例子，假定我们创建一个新的struct fox，并把它加入到fox_lixt，那么我们这样做：
把节点增加到链表尾：

1
list_add_tail(struct list_head *new,struct list_head *head)

该函数向指定链表的head节点前插入new节点。和list_add()函数类似，因为链表是环形的，所以可以把任何一个节点当作head。如果把第一个元素当作head的话，那么该函数可以用来实现一个队列。

从链表中删除一个节点

从链表中增加一个节点之后，从中删除一个节点是另外一个重要的操作。从链表中删除一个节点，调用list_del()：

1
list_del(struct list_head *entry)

该函数从链表中删除entry元素。注意，该操作并不会释放entry或释放包含entry的数据结构体所占用的内存；该函数仅仅是将entry元素从链表中移走，所以该函数被调用之后，通常还需要再撤销包含entry的数据结构体和其中的entry项。
例如，为了删除for节点，我们回到前面增加节点的fox_list：

1
list_del(&f->list)

注意该函数并没有接受fox_list作为输入参数。它只是接受一个特定的节点，并修改其前后节点的指针，这样给定的节点就从链表中删除。代码的实现颇具启发性：

1
2
3
4
5
6
7
8
9
10
static inline void __list_del(struct list_head *prev,struct list_head *next)
{
    next->prev = prev;
    prev->next = next;
}

static inline void list_del(struct list_head *entry)
{
    __list_del(entry->prev,entry->next);
}

从链表中删除一个节点并对其重新初始化：

1
2
list_del_init();
list_del_init(struct list_head *entry);

该函数除了还需要再次初始化entry外，其他和list_del()函数类似。这样做是因为：虽然链表不再需要entry项，但是还是可以再次使用包含entry的数据结构体。

移动和合并链表节点

把节点从一个链表移到另一个链表：

1
list_move(struct list_head *list,struct list_head *head)

该函数从一个链表移除list项，然后将其加入到另一链表的head节点后面。
把节点从一个链表移到另一个链表的末尾：

1
list_move_tail(struct list_head *list,struct list_head *head)

该函数和list_move()函数一样，唯一的不同就是将list项插入到head项前。
检查链表是否为空：

1
list_empty(struct list_head *head)

如果指定的链表为空，该函数返回非0值；否则返回0.
把两个未连接的链表合并在一起：

1
list_splice(struct list_head *list,struct list_head *head)

该函数合并两个链表，它将list指向的链表插入到指定链表的head元素后面。
把两个未连接的链表合并在一起，并重新初始化原来的链表：

1
list_splice_init(struct list_head *list,struct list_head *head)

该函数和list_splice()函数一样，唯一的不同就是由list指向的链表要被重新初始化。

节约两次提领（dereference）
如果你碰巧已经得到next和prev指针，你可以直接调用内部链表函数，从而省下一点时间（其实就是提领指针的时间）。前面讨论的所有函数其实没有做什么其他特别的操作，它仅仅是找到next和prev指针，再去调用内部函数而已。内部函数和它们的外部包装函数同名，仅仅在前面加了两条下划线。比如，可以调用__list_del(prev,next)函数代替调用list_del(list)函数。但这只有在向前向后指针确实已经被提领的情况下才有意义。否则，你只是在画蛇添足。

遍历链表

现在你已经知道了如何在内核中声明、初始化和操作一个链表。这很了不起，但如果无法访问自己的数据，这些没有任何意义。链表仅仅是个能够包含重要数据的容器；我们必须利用链表移动并访问包含我们数据的结构体。幸好，内核为我们提供了一组非常棒的接口，可以用来遍历链表和引用链表中的数据结构体。
注意
和链表操作函数不同，遍历链表的复杂度为O(n)，n是链表所包含的元素数目。

基本方法

遍历链表最简单的方法是使用list_for_each()宏，该宏使用两个list_add()类型的参数，第一个参数用来指向当前项，这是一个你必须要提供的临时变量，第二个参数是需要遍历的链表的以头节点形式存在的list_head。每次遍历中，第一个参数在链表中不断移动指向下一个元素，直到链表中的所有元素都被访问为止。方法如下：

1
2
3
4
struct list_head *p;
list_for_each(p,list) {
    //p指向链表中的元素
}

好了实话实说，其实一个指向链表结构的指针通常是无用的；我们所需要的是一个指向包含list_head的结构体的指针。比如前面的fox结构体的例子，我们需要的是指向每个fox的指针，而不需要指向结构体list成员的指针。我们可以使用前面讨论的list_entry()宏，来获得包含给定list_head()的数据结构。比如：

1
2
3
4
5
6
7
struct list_head *p;
struct fox *f;

list_for_each(p,&fox_list) {
    //f points to the structure in which the list is embedded
    f = list_entry(p,struct fox,list);
}

可用的方法

前面的方法虽然确实展示了list_head节点的功效，但并不优美，而且也不够灵活。所以多数内核代码采用list_for_each_entry()宏遍历链表。该宏内部也使用list_entry()宏，但简化了遍历过程：

1
list_for_each_entry(pos,head,member)

这里pos是一个指向包含list_head节点对象的指针，可将它看作是list_entry()宏的返回值。head是一个指向头节点的指针，即遍历开始位置–在我们前面的例子中，fox_list.member送是pos中list_head结构的变量名。这听起来令人迷惑，但是简单实用。下面的代码片段展示了如何重写前面的list_for_each()，来遍历所有fox节点：

1
2
3
4
5
struct fox *f;

list_for_each_entry(f,&fox_list,list) {
    //on each iteration,'f' points to the next for structure
}

现在看看实际例子吧。它来自inotify–内核文件系统的更新通知机制：

1
2
3
4
5
6
7
8
9
10
11
12
static struct inotify_watch *inode_find_handle(struct inode *inode,
                                               struct inotify_handle *ih)
{
    struct inotify_watch *watch;

    list_for_each_entry(watch,&inode->inotify_watches,i_list) {
        if(watch->ih == ih)
            return watch;
    }
    
    return NULL;
}

该函数遍历了inode->inotify_watches链表中的所有项，每个项的类型都是struct inotify_watch，list_head在结构中被命名为i_list。循环中的每一个遍历，watch都指向链表的新节点。该函数的目的在于：在inode结构串联起来的inotify_wwatches链表中，搜寻其inotify_handle与所提供的句柄相匹配的inotify_watch项。

反向遍历链表

宏list_for_each_entry_reverse()的工作和list_for_each_entry()类似，不同点在于它是反向遍历链表的。也就是说，不再是沿着next指针向前遍历，而是沿着prev指针向后遍历。其用法和list_for_each_entry()相同：

1
list_for_each_entry_reverse(pos,head,member)

很多原因会需要反向遍历链表，其中一个是性能原因–如果你要寻找的节点最可能在你搜索的起始点的前面，那么反向搜索岂不是更快。第二个原因是如果顺序很重要，比如，如果你使用链表实现堆栈，那么你需要从尾部向前遍历才能达到先进先出原则（LIFO）。如果你没有确切的反向遍历的原因，就老实点，用list_for_each_entry()宏吧。

遍历的同时删除

标准的遍历方法在你遍历链表的同时想要删除节点是不行的。因为标准的链表方法建立在你的操作不会改变链表项这一假设上面，所以如果当前项在遍历循环中被删除，那么接下来的遍历就无法获得next（或prev）指针了。这其实是循环处理中的一个常见范式，开发人员通过在潜在的删除操作之前存储next（或prev）指针到一个临时变量中，以便能执行删除操作。好在Linux内核提供了例程处理这种情况：

1
list_for_each_entry_safe(pos,next,head,member)

你可以按照list_for_each_entry()宏的方式使用上述例程，只是需要通过next指针，next指针和pos是同样的类型。list_for_each_entry_safe()启用next指针来将下一项存进表中，以使得能安全删除当前项。我们再次看看inotify的例子：

1
2
3
4
5
6
7
8
9
10
11
12
13
void inotify_node_is_dead(struct inode *inode)
{
    struct inotify_watch *watch,*next;

    mutex_lock(&inode->inotify_mutex);
    list_for_each_entry_safe(watch,next,&inode->inotify_watches,i_list) {
        struct inotify_handle *ih = watch->ih;
        mutex_lock(&ih->mutex);
        inotify_remove_watch_locked(ih,watch);
        mutex_unlock(&ih->mutex);
    }
    mutex_unlock(&inode->inotify_mutex);
}

该函数遍历并删除inotify_watches链表中的所有项。如果使用了标准的list_for_each_entry()，那么上述代码会造成“使用–在–释放后”的错误，因为在移向链表中下一项时，需要访问watch，但这时它已经被撤销。
如果你需要在反向遍历链表的同时删除它，那么内核提供了list_for_each_safe_reverse()宏帮你完成此任务：

1
list_for_each_entry_safe_reverse(pos,n,head,member)

上述函数的用法同list_for_each_entry_safe()。

你仍然需要锁定！
list_for_each_entry()的安全版本只能保护你在循环体中从链表中删除数据。如果这时有可能从其他地方并发进行删除，或者有其他任何并发的链表操作，你就需要锁定链表。

其他链表方法

Linux提供了很多链表操作方法–几乎就是你所能想到的所有访问和操作链表方法，所有这些方法都可在头文件<Linux/list.h>中找到。

队列

任何操作系统内核都少不了一种编程模型：生产者和消费者。在该模式中，生产者创造数据（比如说需要读取的错误信息或者需要处理的网络包），而消费者则反过来，读取消息和处理包，或者以其他方式消费这些数据。实现该模型的最简单的方式无非是使用队列。生产者将数据推进队列，然后消费者从队列中摘取数据。消费者获取数据的顺序和推入队列的顺序一致。也就是说，第一个进入队列的数据一定是第一个离开队列的。也正是这个原因，队列也称为FIFO。顾名思义，FIFO就是先进先出的缩写。下图是一个标准队列的例子。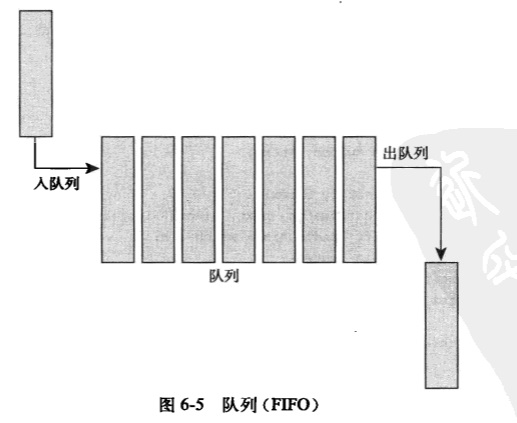
img not found
Linux内核通用队列实现称为kfifo。它实现在文件kernel/kfifo.c中，声明在文件<linux/kfifo.h>中。本节讨论的是自2.66.33以后更新的API，使用方法和2.6.33前的内核稍有不同，所以在使用前请仔细检查文件<linux/kfifo.h>。

kfifo

Linux的kfifo和多数其他队列实现类似，提供了两个主要操作：enqueue（入队列）和dequeue（出队列）。kfifo对象维护了两个偏移量：入口偏移和出口偏移。入口偏移是指下一次入队时的位置，出口偏移是指下一次出队列时的位置。出口偏移总是小于等于入口偏移，否则无意义，因为那样说明要出队列的元素根本还没有入队列。
enqueue操作拷贝数据到队列中的入口偏移位置。当上述动作完成后，入口偏移随之加上推入的元素数目。dequeue操作从队列中出口偏移处拷贝数据，当上述动作完成之后，出口偏移随之减去摘取的元素数目。当出口偏移等于入口偏移时，说明队列空了：在新数据被推入之前，不可再摘取任何数据了。当入口偏移等于队列长度时，说明在队列空置之前，不可再有新数据推入队列。

创建队列

使用kfifo前，首先必须对它进行定义和初始化。和多数内核对象一样，有动态或静态方法供你选择。动态方法更为普遍：

1
int kfifo_alloc(struct kfifo *fifo,unsigned int size,gfp_t gfp_mask);

该函数创建并初始化一个大小为size的kfifo。内核使用gfp_mask标识分配队列。如果成功，kfifo_alloc返回0；错误则返回一个负数错误码。下面便是一个例子：

1
2
3
4
5
6
7
struct kfifo fifo;
int ret;

ret = kfifo_alloc(&kfifo,PAGE_SIZE,GFP_KERNEL);
if(ret)
    return ret;
//fifo现在代表一个大小为PAGE_SIZE的队列

你要想自己分配缓冲，可以调用：

1
void kfifo_init(struct kfifo *fifo,void *buffer,unsigned int size);

该函数创建并初始化一个kfifo对象，它将使用由buffer指向的size字节大小的内存。对于kfifo_alloc()和kfifo_init()，size必须是2的幂。
静态声明kfifo更简单，但不大常用：

1
2
DECLARE_KFIFO(name,size);
INTI_KFIFO(name);

上述方法会创建一个名称为name、大小为size的kfifo对象。和前面一样，size必须是2的幂。

推入队列数据

当你的kfifo对象创建和初始化之后，推入数据到队列需要通过kfifo_in()方法完成：

1
unsigned int kfifo_in(struct kfifo *fifo,const void *from,unsigned int len);

该函数把from指针所指的字节数据拷贝到fifo所指的队列中，如果成功，则返回推入数据的字节大小。如果队列中的空闲字节小于len，则该函数值最多可拷贝队列可用空间那么多的数据，这样的话，返回值可能小于len，甚至返回0，这时意味着没有任何数据被推入。

摘取队列数据

推入数据使用函数kfifo_in()，摘取数据则需要通过函数kfifo_out完成：

1
unsigned int kfifo_out(struct kfifo *fifo,void **to,unsigned int len);

该函数从fifo指向的队列中拷贝出长度为len字节的数据到to所指向的缓存中。如果成功，该函数则返回拷贝的数据长度。如果队列中数据大小小于len，则该函数拷贝出的数据必然小于需要的数据大小。
当数据被摘取之后，数据就不再存在于队列之中。这是队列操作的常用方式。不过如果仅仅想“偷窥”队列中的数据，而不像真的删除它，你可以使用kfifo_out_peek()方法：

1
unsigned int kfifo_out_peek(struct kfifo *fifo,void *to,unsigned int len,unsigned offset);

该函数与kfifo_out类似，但出口偏移不增加，而且摘取的数据仍然可被下次kfifo_out获得。参数offset指向队列中的索引位置，如果该参数为0，则读队列头，这和kfifo_out()无异。

获取队列长度

若想获得用于存储kfifo队列的空间的总体大小（以字节为单位），可调用方法kfifo_size()：

1
static inline unsigned int kfifo_size(struct kfifo *fifo);

另一个内核命名不佳的例子来了–kfifo_len()方法返回kfifo队列中已推入的数据大小：

1
static inline unsigned int kfifo_len(struct kfifo *fifo);

如果想要得到kfifo队列中还有多少可用空间，则要调用方法：

1
static inline unsigned int kfifo_avail(struct kfifo *fifo);

最后两个方法是kfifo_is_empty()和kfifo_is_full()。如果给定的kfifo分别是空或者满，它们返回非0值。如果返回0，则相反。

1
2
static inline int kfifo_is_empty(struct kfifo *fifo);
static inline int kfifo_is_full(struct kfifo *fifo);

重置和撤销队列

如果重置kfifo，意味着抛弃所有队列中的内容，调用kfifo_reset()：

1
static inline void kfifo_reset(struct kfifo *fifo);

撤销一个使用kfifo_alloc分配的队列，调用kfifo_free()：

1
void kfifo_free(struct kfifo *fifo);

如果你是使用kfifo_init()方法创建的队列，那么你需要负责释放相关的缓冲。具体方法取决于你是如何创建它的。

队列使用举例

使用上述接口，我们去看一个kfifo的具体用例。假定我们创建了一个有fifo指向的8KB大小的kfifo。我们就可以推入数据到队列中。这个例子中，我们推入简单的整形数。在你自己的代码中，可以推入更复杂的任务相关数据。这里使用整数，我们看看kfifo如何工作：

1
2
3
4
5
unsigned int i;

//将[0,32]压入到名为“fifo”的kfifo中
for(i = 0;i < 32;i++)
    kfifo_in(fifo,&i,sizeof(i));

名为fifo的kfifo现在包含了0到31的整数，我们查看一下队列的第一个元素是不是0：

1
2
3
4
5
6
7
unsigned int val;
int ret;

ret = kfifo_out_peek(fifo,&val,sizeof(val),0);
if(ret != sizeof(val))
    return  -EINVAL;
printk(KERN_INFO"%u\n",val);//应该输出0

摘取并打印kfifo中的所有元素，我们可以调用kfifo_out()：

1
2
3
4
5
6
7
8
9
10
11
12
//当队列中还有数据时
while(kfifo_avail(fifo)) {
    unsigned int val;
    int ret;

    //read it,one intager at a time
    ret = kfifo_out(fifo,&val,sizeof(val));
    if(ret != sizeof(val))
        return -EINVAL;

    printk(KERN_INFO"%u\n",val);
}

0到31的整数将一一按序打印出来。

映射

一个映射，也常称为关联数组，其实是一个由唯一键组成的集合，而每个键必然关联一个特定的值。这种键到值的关联关系称为映射。映射要至少支持三个操作：

1
2
3
Add(key,value)
Remove(key)
value = Lookup(key)

虽然散列表是一种映射，但并非所有的映射都需要通过散列表实现。除了使用散列表之外，映射也可以通过自平衡二叉搜索树存储数据。虽然散列表能提供更好的平均的渐近复杂度，但是二叉搜索树在最坏情况下能有更好的表现。二叉搜索树同时满足顺序保证，这将给用户的按序遍历带来很好的性能。二叉搜索树的最后一个优势是它不需要散列函数，需要的键类型只要可以定义<=操作算子便可以。
虽然键到值的映射属于一个通用说法，但是更多时候特指使用二叉树而非散列表实现的关联数组。比如，C++的STL容器std::map便是采用自平衡二叉搜索树实现的，它能提供按序遍历的功能。
Linux内核提供了简单的、有效的映射数据结构。但是它不是一个通用的映射结构。因为它的目标是：映射一个唯一的标识数（UID）到一个指针。除了提供三个标准的映射操作之外，Linux还在add操作基础上实现了allocate操作。这个allocate操作不但向map中加入了键值对，而且还可以产生UID。
idr数据结构用于映射用户空间的UID，比如将inotify watch的描述符或者POSIX的定时器ID映射到内核中相关联的数据结构上，如inotify_watch或k_itimer结构体。其命名依然沿袭了内核中有些含混不清的命名体系，这个映射被命名为idr。

初始化一个idr

建立一个idr很简单，首先你需要静态定义或者动态分配一个idr数据结构。然后调用idr_init()：

1
void idr_init(struct idr *idp);

比如：

1
2
struct idr id_huh;//静态定义idr结构
idr_init(&idr_huh);//初始化idr结构

分配一个新的UID

一旦建立了idr，就可以分配新的UID了，这个过程分两步完成。第一步，告诉idr你需要分配新的UID，允许其在必要时调整后备树的大小。然后，第二步才是真正请求新的UID。之所以需要这两个组合动作是因为要允许调整初始大小–这中间涉及在无锁情况下分配内存的场景。
第一个调整后备树大小的方法是idr_pre_get()：

1
int idr_pre_get(struct idr *idp,gfp_t gtp_mask);

该函数将在需要时进行UID的分配工作：调整由idp指向的idr的大小。如果真的需要调整大小，则内存分配例程使用gfp标识：gfp_mask，你不需要对并发访问该方法进行同步保护。和内核中其他函数的做法相反，idr_pre_get()成功时返回1，失败时返回0–这点一定要注意。
第二个函数，实际执行获取新的UID，并且将其加到idr的方法是idr_get_new()：

1
int idr_get_new(struct idr *idp,void *ptr,int *id);

该方法使用idp所指向的idr去分配一个新的UID，并且将其关联到指针ptr上。成功时，该方法返回0，并且将新的UID存于id。错误时，返回非0的错误码，错误码是-EAGAIN，说明你需要再次调用idr_get_new()；如果idr已满，错误码是-ENOSPC。下面看一个完整的例子：

1
2
3
4
5
6
7
int id;

do {
    if(!idr_ptr_get(&idr_huh,GFP_KERNRL))
        return -ENOSPC;
    ret = idr_get_new(&idr_huh,ptr,&id);
}while(ret == -EAGAIN);

如果成功，上述代码片段将获得一个新的UID，它被存储在整型变量id中，而且将UID映射到ptr。
函数idr_get_new_above()使得调用者可以指定一个最小的UID返回值：

1
int idr_get_new_above(struct idr *idp,void *ptr,int starting_id,int *id);

该函数的作用和idr_get_new()相同，除了它确保新的UID大于或等于starting_id外。使用这个变种方法允许idr的使用者确保UID不会被重用，允许其值不但在当前分配的ID中唯一，而且还保证在系统的整个运行期间唯一，下面的代码片段和前例中类似，不过我们明确要求增加UID的值：

1
2
3
4
5
6
7
8
9
10
int id;

do {
    if(!idr_pre_get(&idr_huh,GFP_KERNRL))
        return -ENOSPC;
    ret = idr_get_new_above(&idr_huh,ptr,next_id,&id); 
}while(ret == -EAGAIN);

if(!ret)
    next_id = id + 1;

查找UID

当我们在一个idr中已经分配了一些UID时，我们自然就需要查找它们：调用者要给出UID，idr将返回对应的指针。查找步骤显然要比分配一个新的UID要来的简单，仅需要使用idr_find()方法即可：

1
void *idr_find(struct idr *idp,int id);

该函数如果调用成功，则返回id关联的指针；如果错误，则返回空指针。注意，如果你使用idr_get_new()或者idr_get_new_above()将空指针映射给UID，那么该函数在成功时也返回NULL。这样你就无法区分时成功还是失败，所以，最好不要将UID映射到空指针上。
这个函数的使用比较简单：

1
2
3
struct ma_struct *ptr = idr_find(&idr_huh,id);
if(!ptr)
    return -EINVAL;//错误

删除UID

从idr中删除UID使用方法idr_remove()：

1
void idr_remove(struct idr *idp,int id);

如果idr_remove()成功，则将id关联的指针一起从映射中删除。遗憾的是，idr_remove()并没有办法提示任何错误。

撤销idr

撤销一个idr的操作很简单，调用idr_destroy()函数即可：

1
void idr_destroy(struct idr *idp);

如果该方法成功，则只释放idr中未使用的内存。它并不释放当前分配给UID使用的任何内存。通常，内核代码不会撤销idr，除非关闭或者卸载，而且只有在没有其他用户是才能删除，但是你可以调用idr_remove_all()方法强制删除所有的UID：

1
void idr_remove_all(struct idr *idp);

你应该首先对idp指向的idr调用idr_remove_all()，然后再调用idr_destroy()，这样就能使idr占用的内存都被释放。

二叉树

树结构是一个能提供分层的树形数据结构的特定数据结构。在数学意义上，树是一个无环的、连接的有向图，其中任何一个顶点具有0个或者多个出边以及0个或者1个入边。一个二叉树是每个节点最多具有2个出边的树–也就是，一个树，其节点具有0个、1个或者2个子节点。

二叉搜索树

一个二叉搜索树（BST）是一个节点有序的二叉树，其顺序通常遵循下列法则：

  1. 根的左分支节点值都小于根节点值。
  2. 右分支节点值都大于根节点值。
  3. 所有的子树也都是二叉搜索树。

因此，一个二叉搜索树所有节点都必然有序，且左子节点小于其父节点值，而右子节点大于其父节点值的二叉树。所以，在树中搜索一个给定值或者按序遍历树都相当快捷。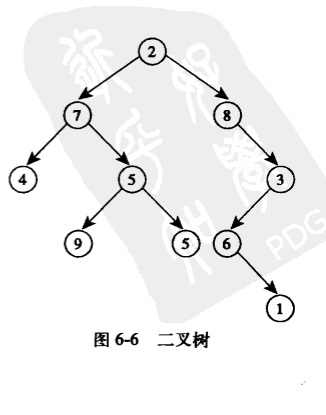
img not found

自平衡二叉搜索树

一个节点的深度是指从其根节点起，到达它一共需要经过的父节点数目。处于树底层的节点称为叶子节点。一个树的高度是指树中的处于最底层的节点的深度。一个平衡二叉搜索树是一个所有叶子节点深度差不超过1的二叉搜索树。一个自平衡二叉搜索树是指其操作都试图维持平衡的二叉搜索树。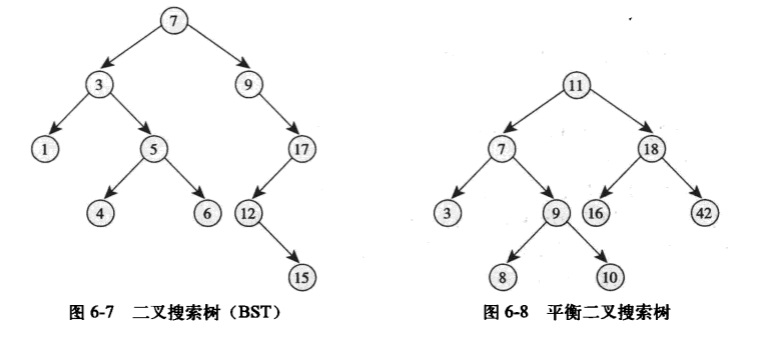
img not found

红黑树

红黑树是一种自平衡二叉搜索树。Linux主要的平衡二叉树数据结构就是红黑树。红黑树具有特殊的着色属性，或红色或黑色。红黑树因遵循下面6个属性，所以能维持半平衡结构：

  1. 所有的节点要么是着红色，要么是着黑色。
  2. 叶子节点都是黑色。
  3. 叶子节点不包含数据。
  4. 所有非叶子节点都有两个子节点。
  5. 如果一个节点是红色，则它的子节点都是黑色。
  6. 在一个节点到其叶子节点的路径中，如果总是包含相同数目的黑色节点，则该路径相比其他路径是最短的。

上述条件，保证了最深的叶子节点的深度不会大于两倍的最浅叶子节点的深度。所以，红黑树总是半平衡的。为什么它具有如此神奇的特点？首先，第五个属性，一个红色节点不能是其他红色节点的子节点或者父节点。而第六个属性保证了从树的任何节点到其叶子节点的路径都具有相同数目的黑色节点，树里的最长路径则是红黑交替节点路径，所以最短路径必然是具有相同数量黑色节点的–只包含黑色节点的路径。于是从根节点到叶子节点的最长路径不会超过最短路劲的两倍。
如果插入和删除操作可以遵循上述六个要求，那这个树会始终保持是一个半平衡树。看起来也许有些奇怪，为什么插入和删除动作都需要服从这些特别的约束，为什么不能用一些简单的规则去维持平衡树呢？其实，实践证明这些规则遵循起来还是相对简单的（实现复杂），而且在保证半平衡树的前提下，这些插入和删除动作并不会增加额外负担。
至于如何让插入和删除动作都能遵循这些规则，请参考相关的数据结构书籍。

rbtree

Linux实现的红黑树称为rbtree。其定义在文件lib/rbtree.c中，声明在文件<linux/rbtree.h>中。除了一定的优化外，Linux的rbtree类似于前面所描述的经典红黑树，即保持了平衡性，所以插入效率和树中节点数目呈对数关系。
rbtree的根节点由数据结构rb_root描述。创建一个红黑树，我们要分配一个新的rb_root结构，并且需要初始化为特殊值RB_ROOT：

1
struct rb_root root = RB_ROOT;

树里的其他节点由rb_node描述。给定一个rb_node，我们可以通过跟踪同名节点指针来找到它的左右子节点。
rbtree的实现并没有提供插入和搜索例程，这些例程希望由rbtree的用户自己定义。这是因为C语言不大容易进行泛型编程，同时Linux内核开发者们相信最有效的搜索和插入方法需要每个用户自己去实现。你可以使用rbtree提供的辅助函数，但你自己要实现比较操作算子。
搜索操作和插入操作最好的范例就是展示一个实际场景：我们先来看搜索，下面的函数实现了在页高速缓存中搜索一个文件区（由一个i节点和一个偏移量共同描述）。每个i节点都有自己的rbtree，以关联在文件中的页偏移。该函数将搜索给定
i节点的rbtree，以寻找匹配的偏移值：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
struct page *rb_search_page_cache(struct inode *inode
                                  unsigned long offset)
{
    struct rb_node *n = inode->i_rb_page_cache.rb_node;

    while(n) {
        struct page *page = rb_entry(n,struct page,rb_page_cache);
        if(offset < page->offset)
            n = n->rb_left;
        else if(offset > page->offset)
            n = n->rb_right;
        else
            return page;
    }
    return NULL;
}

这个例子中，在while循环中遍历了整个rbtree。offset将决定是向左或者向右遍历。if和else条件实际上实现了rbtree的比较方法，从而确保了树的有序性。如果循环中找到了一个匹配offset的节点，则搜索完成，并返回对应的page结构。如果循环查找了全树也没有找到一个匹配项，说明树中不存在匹配项，则函数返回NULL。
插入操作要相对复杂一点，因为必须实现搜索和插入逻辑。下面并非一个了不起的函数，但是可以作为你实现自己的插入操作的一个指导：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
struct page *rb_insert_page_cache(struct inode *inode,
                                  unsigned long offset,
                                  struct rb_node *node)
{
    struct rb_node **p = &inode->i_rb_page_cache.rb_node;
    struct rb_node *parent = NULL;
    struct page *page;

    while(*p) {
        parent = *p;
        page = rb_entry(parent,struct page,rb_page_cache);

        if(offset < page->offset)
            p = &(*p)->rb_left;
        else if(offset > page->offset)
            p = &(*p)->rb_right;
        else
            return page;
    }
    
    rb_link_node(node,parent,p);
    rb_insert_color(node,&inode->i_rb_page_cache);

    return NULL;
}

和搜索操作一样，while循环需要遍历整个树，也是根据offset选择遍历方向。但是和搜索不同的是，该函数希望找不到匹配的offset，因为它想要找的是新offset要插入的叶子节点。当插入点找到之后，调用rb_link_node()在给定位置插入新节点。接着调用rb_insert_color()方法执行复杂的再平衡动作。如果页被加入到页高速缓存中，则返回NULL。如果页已经再高速缓存了，则返回这个已存在的页结构地址。

数据结构以及选择

我们已经详细讨论了Linux中最重要的四种数据结构：链表、队列、映射和红黑树。在本节中，我们将教你如何在代码中具体选择使用哪种数据结构。
如果你对数据集合的主要操作是遍历数据，就使用链表。事实上没有数据结构可以提供比线性算法复杂度更好的算法遍历元素，所以你应该用最简单的数据结构完成简单工作。另外，当性能并非首要考虑因素时，或者当你需要存储相对较少的数据项时，或者当你需要和内核中其他使用链表的代码交互时，也该优先选择链表。
如果你的代码符合生产者/消费者模式，则使用队列，特别是你想（或者可以）要一个定长缓冲。队列会使得添加和删除项的工作简单有效。同时队列也提供了先入先出（FIFO）语义，而这也正是生产者/消费者用例的普遍需求。另一方面，如果你需要存储一个大小不明的数据集合，那么链表可能更合适，因为你可以动态添加任何数量的数据项。
如果你需要映射一个UID到一个对象，就使用映射。映射结构使得映射工作简单有效，而且映射可以帮你维护和分配UID。Linux的映射接口是针对UID到指针的映射，它并不适合其他场景。但是如果你在处理发给用户空间的描述符，就考虑一下映射吧。
如果你需要存储大量数据，并且检索迅速，那么红黑树最好。红黑树可确保搜索时间复杂度是对数关系，同时也能保证按序遍历时间复杂度是线性关系。虽然它比其他数据结构复杂一点，但其对内存开销情况并不是太糟。但是如果你没有执行太多次时间紧迫的查找操作，则红黑树可能不是最好选择。这种情况最好使用链表。
要是上述数据结构都不能满足你的需要，内核还实现了一些较少使用的数据结构，也许它们能帮助你。比如基树（trie）和位图。只有当寻遍所有内核提供的数据结构都不能满足时，你才需要自己设计数据结构。经常在独立的源文件中实现的一种常见的数据结构是散列表。因为散列表无非是一些“桶”和一个散列函数，而且这个散列函数是针对每个用例的，因此用非泛型编程语言（C语言）实现内核范围内的统一散列表，其实这并没有什么价值。

算法复杂度

在计算机和相关的学科中，很有必要将算法的复杂度（或伸缩度）量化的表示出来。虽然存在各种各样表示伸缩度的方法，但最常用的技术还是研究算法的渐近行为。渐近行为是指当算法的输入变得非常大或接近于无限大时算法的行为。渐近行为充分显式了当一个算法的输入逐渐变大时，该算法的伸缩度如何。研究算法的伸缩度（当输入增大时算法执行的变化）可以帮助我们以特定基准抽象出算法模型，从而更好地理解算法的行为。

算法

算法就是一系列的指令，它可能有一个或多个输入，最后产生一个结果或输出。比如计算一个房间中人数的步骤就是一个算法，它的输入是人，计算结果是输出。在Linux内核中，页换出和进程调度都是算法的例子。从数学角度讲，一个算法好比一个函数（或至少我们可将它抽象为一个函数）。比如，我们称人数统计算法为f，要统计的人数为x，可以写成下面形式：

1
y = f(x)  人数统计的函数

这里y是统计x个人所需的时间。

大o符号

一种很有用的渐近表示法就是上限–它是一个函数，其值从一个起始点之后总是超过我们所研究的函数的值，也就是说上限增长等于或者快于我们研究的函数。一个特殊符号，大o符号用来描述这种增长率。函数f(x)可写作O(g(x))，读为“f是g的大o”。数学定义形式为：

1
2
如果f(x)是O(g(x))，那么
存在c，x’满足f(x)<=c*g(x)，任意x>x'

换成自然语言就是，完成f(x)的时间总是短于或等于完成g(x)的时间和任意常量（至少，只要输入的x值大于某个初始值x’）的乘积。
从根本上讲，我们需要寻找一个函数，它的行为和我们的算法一样差或更差。这样一来我们就可以通过给该函数送入非常大的输入，然后观察该函数的结果，从而了解我们算法的执行上限。

大θ符号

当大多数人谈论大o符号时，更准确地讲他们谈论的更接近Donald Knuth所描述的大θ符号。从技术角度讲，大o符号适合描述上限，比如7是6的上限，同样道理，9、12、65也都是6的上限。但在后来大多数人谈论函数增长率时，更多说的时最小上限，或抽象出具有上限和下限的函数。算法分析领域之父，Knuth教授，将其描述为大θ符号，并给出了下面的定义：

1
如果f(x)是g(x)的大θ，那么g(x)既是f(x)的上限也是f(x)的下限。

那么，我们也可以说f(x)是g(x)级（order）。级或大θ是理解内核中算法的最重要的数学工具之一。
所以当人们谈论大o符号时，他们往往是谈论大θ。

时间复杂度

比如，再次考虑计算房间里的人数，假设你一秒钟数一个人，那么如果有7个人在房间里，你需要花7秒钟数他们。显然如果有n个人，需要花n秒钟数他们。我们称该算法的复杂度为O(n)。如果任务是在房间里的所有人面前跳舞呢，因为不管你是5个人还是5000个人，跳舞花费的时间都是相同的，所以该任务的复杂度为O(1)。下表给出了常见的复杂度。

O(g(x)) 名称
1 恒量
log n 对数的
n 线性的
n² 平方的
n³ 立方的
2ⁿ 指数的
n! 阶乘

让房间里的所有人相互介绍的复杂度是多少呢？有什么函数抽象这种算法呢？如果介绍一个人需要花费30秒，那么互相介绍10个人花多久呢？介绍100个人又需要花多久呢？理解一个算法在提高工作负载时的表现，是为给定工作选择最好算法的关键。
显然，应避免使用复杂度为O(n!)或O(2ⁿ)的算法，另外，用复杂度为O(1)的函数代替复杂度为O(n)的函数通常都会提高执行性能。但是情况并非总是如此，不能仅仅依靠算法复杂度来判断哪种算法在实际使用中性能最高。回忆一下，指定的O(g(x))，有一个恒量c和g(x)相乘，所以有可能算法复杂度为O(1)的算法需要花费3个小时才能完成任务，而且无论输入多大，总是要花3个小时。这样的话很可能要比复杂度O(n)、但输入很少的算法费时还长。因此我们在比较算法性能时，还需要考虑输入规模。
我们不赞成使用复杂的算法，但是时刻要注意算法的负载和典型输入集合大小的关系。不要为了你根本不需要支持的伸缩度的要求，盲目的去优化算法。

小结

本章我们讨论了许多Linux内核开发者们用于实现从进程调度到设备驱动等内核代码的通用数据结构。你会随着学习的深入，慢慢发现这些数据结构的妙用。你写你自己的内核代码时，记住总是应该重用已经存在的内核基础设施，别去重复早轮子。
我们也介绍了算法复杂度以及测量和标识算法复杂度的工具，其中最值得注意的是大o。贯穿本书，以及Linux内核，大o都是我们评价算法和内核组件在多用户、处理器、进程、网络连接，以及其他环境下伸缩度的重要指标。